Новости и статьи по автозвуку на МАГНИТОЛЕ

  • Вспомнить все. Фильтры. Фаза и ее производная. Отсекая лишнее-2

    Опубликовано 08.08.2010 03:11

    Вот теперь, когда у нас накопилось некоторое количество материала, можно заняться фазой. Надо с самого начала сказать, что давным-давно понятие фазы ввели для обслуживания нужд электротехники.

    Когда сигнал представляет собой чистый синус (хотя степень чистоты бывает разная) фиксированной частоты, то вполне естественно представить его в виде вращающегося вектора, определяемого, как известно, амплитудой (модулем) и фазой (аргументом). Для звукового сигнала, в котором синусы присутствуют лишь в виде разложения, понятие фазы уже не столь наглядно. Однако не менее полезно — хотя бы потому, что звуковые волны от разных источников складываются векторно. А теперь посмотрим, как выглядят фазочастотные характеристики (ФЧХ) фильтров до четвёртого порядка включительно. Нумерация рисунков будет сохраняться сквозная, с прошлого выпуска.
    Начинаем, стало быть, с рис. 12 и 13.


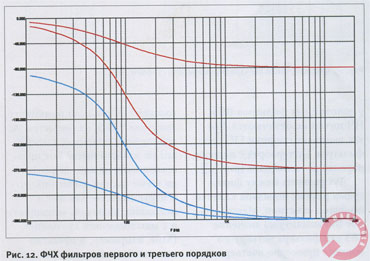
    Сразу можно подметить любопытные закономерности.

    1. Любой фильтр «крутит» фазу на угол, кратный π/4, точнее говоря, на величину (nπ)/4, где n — порядок фильтра.

    2. ФЧХ фильтра НЧ всегда начинается от 0 градусов.

    3. ФЧХ фильтра ВЧ всегда приходит на 360 градусов.

    Последний пункт можно уточнить: «точка назначения» ФЧХ фильтра верхних частот кратна 360 градусам; если порядок фильтра выше четвёртого, то с ростом частоты фаза фильтра ВЧ будет стремиться к 720 градусам, то есть к 4π, если выше восьмого — к 6π и т. д. Но для нас это уже чистая математика, имеющая к практике весьма отдалённое отношение.


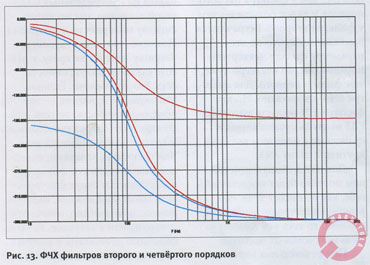
    Из совместного рассмотрения перечисленных трёх пунктов нетрудно заключить, что ФЧХ фильтров ВЧ и НЧ совпадают лишь для чётвёртого, восьмого и т.д. порядков, а справедливость этого утверждения для фильтров четвёртого порядка наглядно подтверждает и график на рис. 13. Впрочем, из этого факта не следует, что фильтр четвёртого порядка «самый лучший», как, кстати, не следует и обратного. И вообще, выводы пока делать рано.
    Фазовые характеристики фильтров не зависят от способа реализации — активные они или пассивные, и даже от физической природы фильтра. Поэтому мы не будем специально заострять внимание на ФЧХ пассивных фильтров, они по большей части ничем не отличаются от тех, что мы уже видели. Кстати говоря, фильтры относятся к числу так называемых минимально-фазовых цепей — их амплитудно-частотные и фазочастотные характеристики жёстко взаимосвязаны. К числу неминимально-фазовых звеньев относится, к примеру, линия задержки.
    Совершенно очевидно (при наличии графиков), что чем выше порядок фильтра, тем его ФЧХ падает круче. А крутизну любой функции характеризуют чем? Её производной. Производная ФЧХ по частоте имеет специальное название — групповое время задержки (ГВЗ). Фазу надо брать в радианах, а частоту — не колебательную (в герцах), а угловую, в радианах в секунду. Тогда производная получит размерность времени, что объясняет (правда, частично) её название. Характеристики ГВЗ у однотипных фильтров ВЧ и НЧ ничем не отличаются. Вот так выглядят графики ГВЗ для фильтров Баттерворта с первого порядка по четвёртый (рис. 14).


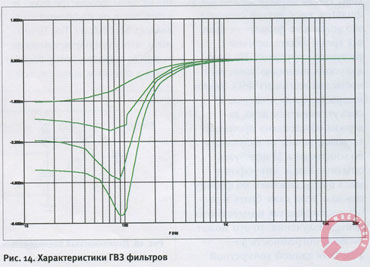
    Тут разница между фильтрами разных порядков кажется особенно заметной. Максимальное (по амплитуде) значение ГВЗ для фильтра четвёртого порядка примерно вчетверо больше, чем у фильтра первого порядка и вдвое больше — чем у фильтра второго. Встречаются высказывания, что по этому параметру фильтр четвёртого порядка как раз вчетверо хуже, чем фильтр первого. Для фильтра ВЧ — возможно. Но для фильтра НЧ минусы высокого ГВЗ не столь существенны в сравнении с плюсами высокой крутизны спада АЧХ.


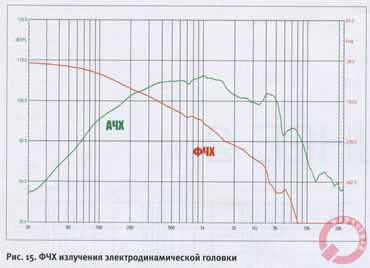
    Для дальнейшего изложения нам полезно будет представлять себе, как выглядит ФЧХ «по воздуху» электродинамической головки, то есть как зависит фаза излучения от частоты.
    Примечательная картинка (рис. 15): на первый взгляд как у фильтра, но, с другой стороны, это вовсе и не фильтр — фаза всё время падает, причём с растущей крутизной. Не буду напускать лишнюю таинственность: так выглядит ФЧХ линии задержки. Люди опытные скажут: понятное дело, задержка обусловлена пробегом звуковой волны от излучателя до микрофона. И ошибутся опытные люди: микрофон у меня был установлен по фланцу головки; если даже брать в расчёт положение так называемого центра излучения, то это может вызвать погрешность 3 — 4 см (для данной конкретной головки). А тут, если прикинуть, задержка почти на полметра. А, собственно, почему её (задержки) не должно быть? Вот представьте себе на выходе усилителя такой сигнал: ничего-ничего, и вдруг синус — как ему и положено, из начала координат и с максимальной крутизной. (Мне, например, и представлять ничего не надо, у меня на одном из измерительных CD такое записано, мы по этому сигналу полярность проверяем.) Понятно, ток через звуковую катушку потечёт не сразу, у неё ещё какая-то индуктивность есть. Но это мелочи. Главное, что звуковое давление — это объёмная скорость, то есть диффузору надо сперва разогнаться, и только потом появится звук. Для величины задержки, наверное, можно вывести формулу, наверняка там будут фигурировать масса «подвижки», силовой фактор и, возможно, омическое сопротивление катушки. Кстати, подобные результаты я получал на разном оборудовании: как на аналоговом фазометре Bruel & Kjaer, так и на цифровых комплексах MLSSA и Clio. Точно знаю, что у среднечастотников задержка меньше, чем у басовиков, а у пищалок меньше, чем у тех и этих. Как ни удивительно, но в литературе я ссылок на подобные результаты не встречал.
    Зачем я привёл этот поучительный график? А затем, что если дело действительно обстоит именно так, как мне видится, то многие рассуждения о свойствах фильтров теряют практический смысл. Хотя я их всё же изложу, а вы уже сами решите, все ли из них стоит принимать на вооружение.

    Схемы пассивных фильтров

    Думаю, мало кто удивится, если я заявлю, что схемных реализаций пассивных фильтров существует куда меньше, чем фильтров активных. Я бы сказал, что их примерно две с половиной. То есть если эллиптические фильтры выводить в отдельный класс схем, получится три, если этого не делать — то две. Причём в 90% случаев в акустике используются так называемые параллельные фильтры. Поэтому мы начнём не с них.
    Последовательные фильтры, в отличие от параллельных, не существуют «по частям» — тут фильтр НЧ, а там фильтр ВЧ. А значит, вы не сможете подключить их к разным усилителям. К тому же по своим характеристикам это фильтры первого порядка. А между прочим, ещё вездесущий господин Смолл обосновал, что фильтры первого порядка для акустических применений непригодны, что бы там ни говорили ортодоксальные аудиофилы (с одной стороны) и сторонники всемерного удешевления акустической продукции (с другой). Однако у последовательных фильтров есть один плюс: сумма выходных напряжений у них всегда равна единице. Вот как выглядит схема двухполосного последовательного фильтра (рис. 16).


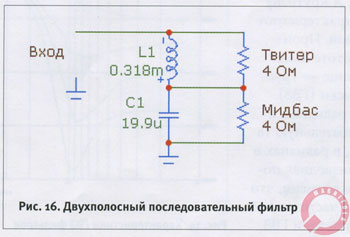
    В данном случае номиналы соответствуют частоте среза 2000 Гц. Нетрудно понять, что сумма напряжений на нагрузках всегда в точности равна входному напряжению. Эта особенность последовательного фильтра используется при «подготовке» сигналов для их дальнейшей обработки процессором (в частности, в Dolby Pro Logic). На следующем графике вы видите АЧХ фильтра (рис. 17).


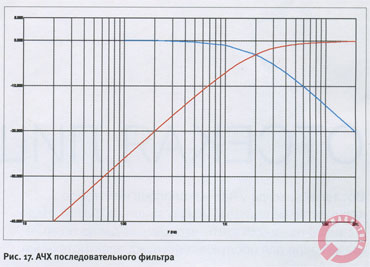
    Можете поверить, что графики ФЧХ и ГВЗ у него точно такие же, как и у любого фильтра первого порядка. Науке известен и трёхполосный последовательный фильтр. Схема его на рис. 18.


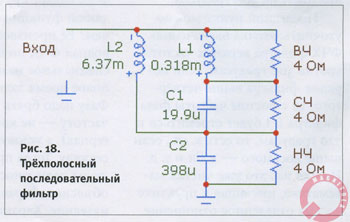
    Приведенные на схеме номиналы соответствуют той же частоте раздела (2000 Гц) между твитером (ВЧ) и среднечастотником и частоте 100 Гц — раздела между СЧ и НЧ-головками. Понятно, что трёхполосный последовательный фильтр обладает тем же свойством: сумма напряжений на его выходе в точности равна напряжению на входе. На следующем рисунке (рис. 19), где приведен набор характеристик этого фильтра, вы можете увидеть, что крутизна спада фильтра пищалки в диапазоне 50 — 200 Гц выше, чем 6 дБ/окт., поскольку его полоса тут накладывается не только на полосу СЧ, но и на полосу НЧ головки. Вот уж чего не умеют делать параллельные фильтры — у них перехлёст полос неизбежно преподносит сюрпризы, и всегда — нерадостные.


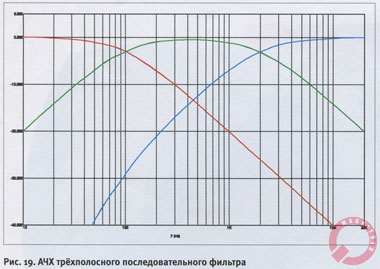
    Параметры последовательного фильтра рассчитываются в точности так же, как и номиналы фильтров первого порядка. Зависимость всё та же (см. формулу 1.1). Удобнее всего ввести так называемую постоянную времени, через частоту среза фильтра она выражается как TO = 1/(2πFc).

    Тогда

    C = TO/RL (2.1), а

    L = TO*RL (2.2).

    (Здесь RL — импеданс нагрузки, в данном случае 4 Ом).

    Если, как во втором случае, у вас трёхполосный фильтр, то частот раздела будет две и постоянных времени тоже две.

    Наверное, самые технически подкованные из вас уже заметили, что я слегка «передёрнул» карты и заменил реальный импеданс нагрузки (то есть динамика) омическим «эквивалентом» 4 Ом. В действительности, конечно, никакой он не эквивалент. На самом деле даже принудительно заторможенная звуковая катушка с точки зрения измерителя импеданса выглядит как последовательно соединённые активное и индуктивное сопротивление. А когда катушка обладает подвижностью, индуктивность возрастает на высокой частоте, а вблизи частоты резонанса головки у неё как бы возрастает омическое сопротивление, случается, и в десять раз, и больше. Программ, которые умеют учитывать такие особенности реальной головки, очень немного, мне лично известно три. Но мы никоим образом не ставили своей целью научиться работать, скажем, в программной среде Linearx. У нас задача иная — разобраться с основными особенностями фильтров. Поэтому будем по старинке имитировать присутствие головки резистивным эквивалентом, и конкретно — номиналом 4 Ом. Если в вашем случае нагрузка имеет другой импеданс, то и все входящие в схему пассивного фильтра импедансы должны быть пропорционально изменены. То есть индуктивности — пропорционально, а ёмкости — обратно пропорционально сопротивлению нагрузки.
    (Прочтя это в черновике, главный редактор сказал: «Ты что, последовательные фильтры — это Клондайк, давай копнём как-нибудь». Согласен. Клондайк. Пришлось обещать, что в одном из грядущих номеров отдельно и специально копнём.)
    Получившие наиболее широкое распространение параллельные фильтры называют ещё «лестничными». Думаю, всем будет ясно, откуда взялось это название после того, как вы взглянете на обобщённую схему фильтра (рис. 20).


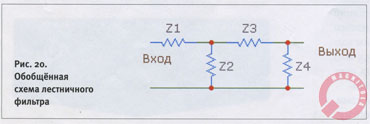
    Чтобы получить фильтр НЧ четвёртого порядка, надо все горизонтальные «планки» в этой схеме заменить индуктивностями, а все вертикальные — емкостями. Соответственно, для построения фильтра ВЧ нужно сделать всё наоборот. Фильтры более низких порядков получаются путём отбрасывания одного или более элементов, начиная с последнего. Фильтры более высокого порядка получают аналогичным способом, только наращиванием числа элементов. Но мы с вами договоримся: выше четвёртого порядка фильтров для нас не существует. Как мы увидим позже, одновременно с ростом крутизны фильтра углубляются и их недостатки, поэтому такая договорённость не является чем-то крамольным. Для полноты изложения надо бы сказать ещё вот что. Существует альтернативный вариант построения пассивных фильтров, где первым элементом всегда ставится резистор, а не реактивный элемент. Такие схемы применяют, когда требуется нормировать входной импеданс фильтра (например, операционные усилители «не любят» нагрузку менее 50 Ом). Но в нашем случае лишний резистор — это неоправданные потери мощности, поэтому «наши» фильтры начинаются реактивностью. Если, конечно, не требуется специально снизить уровень сигнала.
    Самый сложный по устройству полосовой фильтр получается, если в обобщённой схеме каждый горизонтальный элемент заменить последовательным соединением ёмкости и индуктивности (в любой последовательности), а каждый вертикальный элемент должен быть заменён параллельно включёнными — также ёмкостью и индуктивностью. Наверное, я всё-таки приведу такую вот «страшную» схему (рис. 21).


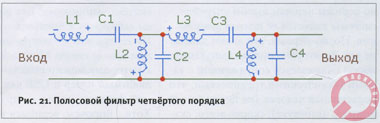
    Есть ещё одна маленькая хитрость. Если вам понадобится несимметричный «бандпасс» (полосовой фильтр), у которого, скажем, фильтр ВЧ имеет четвёртый порядок, а фильтр НЧ — второй, то лишние детали из приведённой выше схемы (то есть один конденсатор и одну катушку) надо убирать непременно с «хвоста» схемы, а не наоборот. Иначе вы получите несколько неожиданные эффекты от изменения характера нагружения предыдущих каскадов фильтра.
    Мы не успели познакомиться с эллиптическими фильтрами. Ну, значит, в следующий раз с них и начнём.

    Источник: журнал Автозвук, 05/2009. Текст: Юрий Евтушенко

    1. Категории:
    2. Журнал АвтоЗвук

  • Предложения партнеров МАГНИТОЛЫ

  cc by-nc-sa