— Как! У тебя есть бабушка, которая угадывает три карты сряду, а ты до сих пор не перенял у ней ее кабалистики?
А.С. Пушкин, «Пиковая дама»
А.С. Пушкин, «Пиковая дама»
Как и было обещано, про мощность закончили, надоело. В своё время к вопросу вернёмся, на другом уровне и под иным предлогом, сегодня речь пойдёт (как тоже было обещано) о том, что важно знать об акустике на самом деле. А именно — о знаменитых параметрах Тиля — Смолла, знание которых — залог выигрыша в азартной игре в автозвук. Без шельмовства и кабалистики.
Что общего у колокола и громкоговорителя? Ну, то, что оба звучат, — это очевидно. Важнее, что и то и другое — колебательные системы. А в чём различие? Колокол, как по нему ни долби, будет звучать на единственной частоте, предписанной каноном. А внешне не так уж непохожий на него динамик — в широком диапазоне частот, и может, при желании, одновременно изобразить и звон колокола, и пыхтение звонаря. Так вот: два из трёх параметров Тиля — Смолла как раз и описывают количественно это различие.
Только надо твёрдо запомнить, а лучше — перечитать цитату из основоположника в историко-биографической справке. Там сказано: «на низких частотах». К тому, как поведёт себя динамик на частотах более высоких, Тиль, Смолл и их параметры никакого отношения не имеют и никакой ответственности за это не несут. Какие частоты для динамика низкие, а какие — нет? А об этом и говорит первый из тройки параметров.
КАРТА ПЕРВАЯ, ИЗМЕРЯЕМАЯ В ГЕРЦАХ
Итак: параметр Тиля — Смолла №1 — собственная резонансная частота динамика. Обозначается всегда Fs, независимо от языка публикации. Физический смысл предельно прост: раз динамик — колебательная система, значит, должна быть частота, на которой диффузор будет колебаться, будучи предоставлен сам себе. Как колокол после удара или струна после щипка. При этом имеется в виду, что динамик абсолютно «голый», не установлен ни в какой корпус, как бы висит в пространстве. Это важно, поскольку нас интересуют параметры собственно динамика, а не того, что его окружает.
Диапазон частот вокруг резонансной, две октавы вверх, две октавы вниз — это и есть область, где действуют параметры Тиля — Смолла. Для сабвуферных головок, ещё не установленных в корпус, Fs может составлять от 20 до 50 Гц, у мидбасовых динамиков от 50 (басовитые «шестёрки») до 100 — 120 («четвёрки»). У диффузорных среднечастотников — 100 — 200 Гц, у купольных — 400 — 800, у пищалок — 1000 — 2000 Гц (бывают исключения, очень редкие).
Как определяют собственную резонансную частоту динамика? Нет, как чаще всего определяют — ясно, читают в сопроводительной документации или в отчёте о тесте. Ну а как её изначально узнали? С колоколом было бы проще: дал по нему чем-нибудь и измерил частоту производимого гудения. Динамик же в явной форме ни на какой частоте гудеть не будет. То есть он хочет, но ему не даёт присущее его конструкции затухание колебаний диффузора. В этом смысле динамик очень сходен с автомобильной подвеской, и этой аналогией я пользовался не раз и ещё буду. Что произойдёт, если качнуть на подвеске автомобиль с пустыми амортизаторами? Он хоть несколько раз, но качнётся на собственной резонансной частоте (где есть пружина, там будет и частота). Амортизаторы, сдохшие только отчасти, остановят колебания после одного-двух периодов, а исправные — после первого же качка. В динамике амортизатор главнее пружины, причём здесь их даже два.
Первый, более слабый, работает благодаря тому, что происходит потеря энергии в подвесе. Не случайно гофр делается из специальных сортов каучука, мячик из такого материала от пола почти не будет отскакивать, специальная пропитка с большим внутренним трением выбирается и для центрирующей шайбы. Это как бы механический тормоз колебаний диффузора. Второй, гораздо более мощный — электрический.
Вот как он работает. Звуковая катушка динамика — его мотор. В ней течёт переменный ток от усилителя, и катушка, находящаяся в магнитном поле, начинает двигаться с частотой подведенного сигнала, двигая, понятно, и всю подвижную систему, затем она и здесь. Но ведь катушка, двигающаяся в магнитном поле — это генератор. Который будет вырабатывать тем больше электричества, чем сильнее движется катушка. И когда частота станет приближаться к резонансной, на которой диффузор «хочет» колебаться, амплитуда колебаний возрастёт, и напряжение, производимое звуковой катушкой, будет расти. Достигнув максимума точно на резонансной частоте. Какое это отношение имеет к торможению? Пока никакого. Но представьте себе, что выводы катушки замкнули между собой. Теперь уже по ней потечёт ток и возникнет сила, которая по школьному правилу Ленца будет препятствовать движению, его породившему. А ведь звуковая катушка в реальной жизни замкнута на выходное сопротивление усилителя, близкое к нулю. Получается как бы электрический тормоз, приспосабливающийся к обстановке: чем с большим размахом пытается ходить туда-сюда диффузор, тем больше этому препятствует встречный ток в звуковой катушке. У колокола тормозов нет, кроме затухания вибраций в его стенках, а в бронзе — какое затухание...
 Один выдающийся математик, по преданию, читая студентам лекции, говорил: «А сейчас мы приступим к доказательству теоремы, имя которой я имею честь носить». Кому выпала честь носить имена параметров Тиля и Смолла? Вспомним и это. Первым в связке идёт Альберт Невил Тиль (в оригинале A. Neville Thiele, «А» почти никогда не расшифровывается). И по возрасту, и по библиографии. Тилю сейчас 84 года, а когда ему было 40, он опубликовал историческую работу, в которой впервые было предложено проводить расчёты характеристик громкоговорителей на основе единого набора параметров, причём удобным и воспроизводимым образом.
Один выдающийся математик, по преданию, читая студентам лекции, говорил: «А сейчас мы приступим к доказательству теоремы, имя которой я имею честь носить». Кому выпала честь носить имена параметров Тиля и Смолла? Вспомним и это. Первым в связке идёт Альберт Невил Тиль (в оригинале A. Neville Thiele, «А» почти никогда не расшифровывается). И по возрасту, и по библиографии. Тилю сейчас 84 года, а когда ему было 40, он опубликовал историческую работу, в которой впервые было предложено проводить расчёты характеристик громкоговорителей на основе единого набора параметров, причём удобным и воспроизводимым образом.Там, в работе 1961 года, было, в частности, сказано: «Характеристики громкоговорителя в области низких частот могут быть адекватно описаны с помощью трёх параметров: резонансной частоты, объёма воздуха, эквивалентного акустической гибкости громкоговорителя, и отношения электрического сопротивления к сопротивлению движению на резонансной частоте. По этим же параметрам определяется и электроакустическая эффективность. Я обращаюсь к производителям громкоговорителей с просьбой публиковать эти параметры как часть основных сведений об их изделиях».
Просьба Невилла Тиля была услышана индустрией только через десятилетие, в это время Тиль уже работал вместе с Рихардом Смоллом, уроженцем Калифорнии. По-калифорнийски пишется Richard Small, но почему-то уважаемый доктор предпочитает немецкий вариант произношения собственного имени. Смоллу в этом году исполняется 70, между прочим — юбилей поважнее многих. В начале семидесятых Тиль и Смолл окончательно довели до ума предложенный ими подход к расчёту громкоговорителей.
Сейчас Невилл Тиль — почётный профессор одного из университетов у себя на родине, в Австралии, а последняя профессиональная позиция Д-ра Смолла, за которой нам удалось уследить — главный инженер департамента автомобильной аудиотехники Harman-Becker. Ну и, само собой, оба — в составе руководства международного общества инженеров-акустиков (Audio Engineering Society). В общем, оба живы здоровы.
КАРТА ВТОРАЯ, НЕ ИЗМЕРЯЕМАЯ НИ В ЧЁМ
Мощность тормозов динамика численно выражается во втором параметре Тиля — Смолла. Это — полная добротность динамика, обозначается Qts. Выражается численно, но не буквально. В смысле, чем мощнее тормоза, тем меньше величина Qts. Отсюда и название «добротность» в русском (или quality factor в английском, из которого возникло обозначение этой величины), что это как бы оценка качества колебательной системы. Физически добротность — отношение упругих сил в системе к вязким, иначе — к силам трения. Упругие силы сохраняют энергию в системе, попеременно перегоняя энергию из потенциальной (сжатая или растянутая пружина или же подвес динамика) в кинетическую (энергия движущегося диффузора). Вязкие норовят энергию любого движения превратить в тепло и безвозвратно рассеять. Высокая добротность (а у того же колокола она будет измеряться десятками тысяч) означает, что упругих сил намного больше, чем сил трения (вязких, это одно и то же). Это же означает, что на каждое колебание в тепло будет переходить только малая часть энергии, запасённой в системе. Поэтому, кстати, добротность — единственная величина в тройке параметров Тиля — Смолла, не имеющая размерности, это отношение одних сил к другим. Как рассеивает энергию колокол? Через внутреннее трение в бронзе, главным образом, потихоньку. Как это делает динамик, у которого добротность намного меньше, а значит, темпы потери энергии гораздо выше? Двумя способами, по числу «тормозов». Часть рассеивается через внутренние потери в упругих элементах подвеса, и эту долю потерь можно оценить отдельной величиной добротности, она носит название механической, обозначается Qms. Вторая, большая часть рассеивается в виде тепла от тока, проходящего по звуковой катушке. Тока, ей же выработанного. Это — электрическая добротность Qes. Суммарное действие тормозов определялось бы очень легко, если бы в ходу были не величины добротности, а наоборот, величины потерь. Мы бы их просто сложили. А раз мы имеем дело с величинами, обратными потерям, то и складывать придётся обратные величины, поэтому и выходит, что 1/Qts = 1/Qms + 1/Qes.
Типичные значения добротностей: механическая — от 5 до 10. Электрическая — от 0,2 до 1. Поскольку в дело идут обратные величины, то получается, что мы суммируем механический вклад в потери порядка 0,1 — 0,2 с электрическим, составляющим от 1 до 5. Ясно, что итог будет определяться в основном электрической добротностью, то есть главный тормоз динамика — электрический.
Так как же вырвать у динамика имена «трёх карт»? Ну хотя бы двух первых, до третьей ещё доберёмся. ####олетом, как Германн, грозить бесполезно, динамик не старуха. На помощь приходит всё та же звуковая катушка, пламенный мотор динамика. Ведь мы уже осознали: пламенный мотор подрабатывает и пламенным генератором. И в этом качестве как бы ябедничает об амплитуде колебаний диффузора. Чем большее напряжение появится на звуковой катушке как результат её колебаний вместе с диффузором, тем больше, значит, размах колебаний, тем ближе, значит, мы к резонансной частоте.
Как это напряжение измерить, притом что к звуковой катушке подведен сигнал от усилителя? То есть как разделить подведенное к мотору от выработанного генератором, это же на одних и тех же выводах? А не надо разделять, надо измерить получающуюся сумму.
Для этого поступают так. Динамик присоединяют к усилителю с возможно большим выходным сопротивлением, в реальной жизни это означает: последовательно с динамиком включают резистор с номиналом намного, в сто, как минимум, раз больше номинального сопротивления динамика. Скажем, 1000 Ом. Теперь при работе динамика звуковая катушка будет вырабатывать противо-ЭДС, вроде как для работы электрического тормоза, но торможения не произойдёт: выводы катушки замкнуты между собой через очень большое сопротивление, ток мизерный, тормоз — никудышный. Зато напряжение, по правилу Ленца противоположное по полярности подведенному («порождающему движение»), сложится с ним в противофазе, и если в этот момент измерить кажущееся сопротивление звуковой катушки, то покажется, что оно очень большое. На самом деле при этом противо-ЭДС не даёт току от усилителя беспрепятственно протекать по катушке, прибор это истолковывает как возросшее сопротивление, а как ещё?
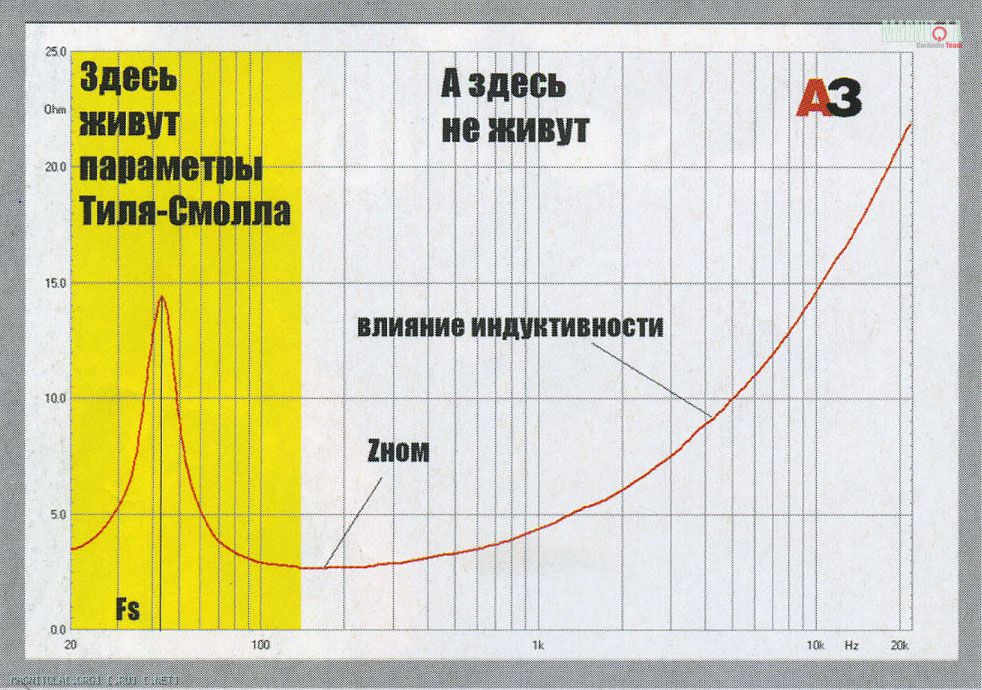
Через измерение импеданса, того самого «кажущегося» (а на деле — комплексного, со всякими активными и реактивными составляющими, сейчас об этом не время) сопротивления и открываются две карты из трёх. Кривая импеданса любого диффузорного динамика, от Келлога и Райса до наших дней, выглядит, в принципе, одинаково, она даже фигурирует в логотипе какого-то электроакустического научного сообщества, сейчас забыл, какого. Горб на низких (для этого динамика) частотах обозначает частоту его основного резонанса. Где максимум — там и вожделенная Fs. Элементарнее не бывает. Выше резонанса наступает минимум полного сопротивления, его-то обычно и принимают за номинальное сопротивление динамика, хотя, как видите, оно остаётся таким только в небольшой полосе частот. Выше полное сопротивление начинает вновь расти, теперь уже из-за того, что звуковая катушка — не только мотор, но и индуктивность, сопротивление которой растёт с частотой. Но туда мы сейчас ходить не будем, там интересующие нас параметры не живут.
Куда сложнее с величиной добротности, но, тем не менее, исчерпывающая информация о «второй карте» тоже содержится в импедансной кривой. Исчерпывающая, потому что по одной кривой можно вычислить и электрическую Qes, и механическую добротность Qms, по отдельности. Как потом сделать из них полную Qts, реально необходимую при расчёте оформления, мы уже знаем, дело нехитрое, не бином Ньютона.
Как именно определяются искомые величины по импедансной кривой, мы обсудим в другой раз, когда разговор пойдёт о методах измерения параметров. Сейчас будем исходить из того, что кто-то (производитель акустики или соратники вашего покорного слуги) это за вас сделали. Но отмечу вот что. Существует два заблуждения, связанных с попытками экспресс-анализа параметров Тиля — Смолла по виду кривой импеданса. Первое — совсем лоховское, его мы сейчас развеем без следа. Это когда глядят на кривую импеданса с огромным горбом на резонансе и восклицают: «Ничего себе добротность!» Типа — высокая. А глядя на маленький пупырышек на кривой, заключают: раз пик импеданса так приглажен, значит, у динамика высокое демпфирование, то есть — низкая добротность.
Так вот: в самом простом варианте это ровно наоборот. Что означает высокий пик импеданса на частоте резонанса? Что звуковая катушка вырабатывает много противо-ЭДС, предназначенной для электрического торможения колебаний диффузора. Только при таком включении, через большое сопротивление, ток, необходимый для работы тормоза, не протекает. А когда такой динамик окажется включён не для измерений, а нормально, напрямую от усилителя, тормозящий ток пойдёт будь здоров, катушка станет могучим препятствием на пути неумеренных колебаний диффузора на его любимой частоте.
При прочих равных можно грубо оценить добротность по кривой, причём именно помня: высота импедансного пика характеризует потенциал электрического тормоза динамика, следовательно, чем он выше, тем НИЖЕ добротность. Будет ли такая оценка исчерпывающей? Не совсем, как было сказано, она останется грубой. Ведь в импедансной кривой, как уже говорилось, закопана информация и о Qes, и о Qms, выкопать которую можно (вручную или с помощью компьютерной программы), проанализировав не только высоту, но и «ширину плеч» резонансного горба. По этому поводу мы тут поставили несколько вычислительных экспериментов, кому интересно — посмотрите.
А как добротность сказывается на форме АЧХ динамика, нас ведь именно это интересует? Как сказывается — решающим образом сказывается. Чем ниже добротность, то есть чем мощнее внутренние тормоза динамика на резонансной частоте, тем ниже и более плавно спадая, пройдёт вблизи резонанса кривая, характеризующая создаваемое динамиком звуковое давление. Минимальная неравномерность в этой полосе частот будет при Qts, равной 0,707, что принято называть характеристикой Баттерворта. При высоких значениях добротности кривая звукового давления начнёт «горбиться» вблизи резонанса, понятно почему: тормоза слабые.
Бывает ли «хорошая» или «плохая» полная добротность? Сама по себе — нет, потому что, когда динамик окажется установлен в акустическое оформление, в качестве которого сейчас будем рассматривать только закрытый ящик, и частота его резонанса, и полная добротность станут другими. Почему? Потому что и то и то зависит от упругости подвеса динамика. Резонансная частота зависит только от массы подвижной системы и жёсткости подвеса. С ростом жёсткости Fs растёт, с ростом массы — падает. Когда динамик установлен в закрытый ящик, воздух в нём, обладающий упругостью, начинает работать дополнительной пружиной в подвесе, общая жёсткость повышается, Fs растёт. Растёт и полная добротность, поскольку она — отношение упругих сил к тормозящим. Возможности тормозов динамика от его установки в некий объём не изменятся (с чего бы?), а суммарная упругость — возрастёт, добротность — неизбежно возрастёт. И никогда не станет ниже, чем была у «голого» динамика. Никогда, это — нижний предел. Насколько всё это возрастёт? А это зависит от того, насколько жёсткий у динамика собственный подвес. Смотрите: одно и то же значение Fs можно получить при лёгком диффузоре на мягком подвесе или при тяжёлом — на жёстком, масса и жёсткость действуют в противоположных направлениях, а итог может оказаться численно равным. Теперь если мы поставим в какой-то объём (обладающий полагающимся этому объёму упругостью) динамик с жёстким подвесом, то он небольшого возрастания суммарной жёсткости и не заметит, величины Fs и Qts изменятся не сильно. Поставим туда же динамик с мягким подвесом, по сравнению с жёсткостью которого «воздушная пружина» будет уже существенной, и увидим, что суммарная жёсткость изменилась сильно, а значит, Fs и Qts, исходно такие же, как у первого динамика, изменятся существенно.
В тёмные «дотилевские» времена для расчёта новых значений частоты резонанса и добротности (они, чтобы не путать с параметрами «голого» динамика, обозначаются как Fc и Qtc) нужно было знать (или измерить) непосредственно упругость подвеса, в миллиметрах на ньютон приложенной силы, знать массу подвижной системы, а потом мудрить с программами расчёта. Тиль предложил концепцию «эквивалентного объёма», то есть такого объёма воздуха в закрытом ящике, упругость которого равна упругости подвеса динамика. Эта величина, обозначаемая Vas, и есть третья волшебная карта.
Итоги вычислительного эксперимента, которые помогут желающим понять, как величины электрической и механической добротности выражаются в импедансных кривых. Мы взяли полный набор электромеханических параметров реально существующего динамика, а потом стали изменять некоторые из них. Сперва — механическую добротность, как будто заменяли материал гофра и центрирующей шайбы. Потом — электрическую, для этого уже понадобилось изменять характеристики привода и подвижной системы. Вот что получилось:
| Реальная импедансная кривая низкочастотного динамика. По ней вычисляются два из трёх главных параметров | |
Кривые импеданса для разных значений полной добротности, при этом электрическая Qes одна и та же, равная 0,5, а механическая изменяется от 1 до 8. Полная добротность Qts изменяется вроде бы не сильно, а высота горба на графике импеданса — сильно, и очень, при этом чем меньше Qms, тем он становится острее | Зависимость звукового давления от частоты при тех же значениях Qts. При измерении звукового давления важна только полная добротность Qts, поэтому совершенно непохожим кривым импеданса соответствуют не такие уж разные кривые звукового давления от частоты |
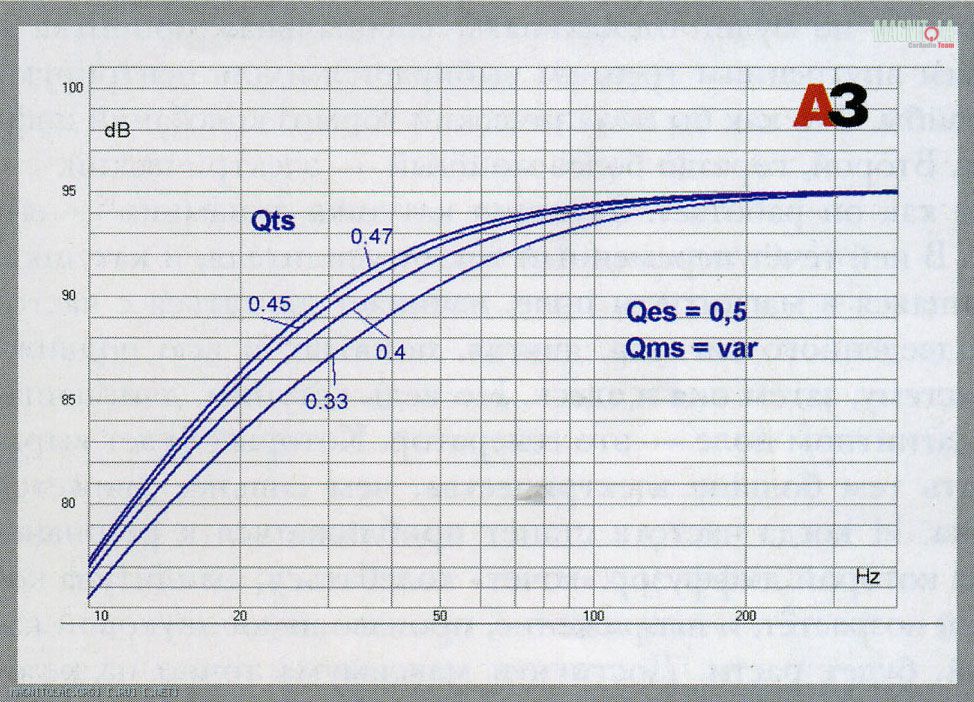
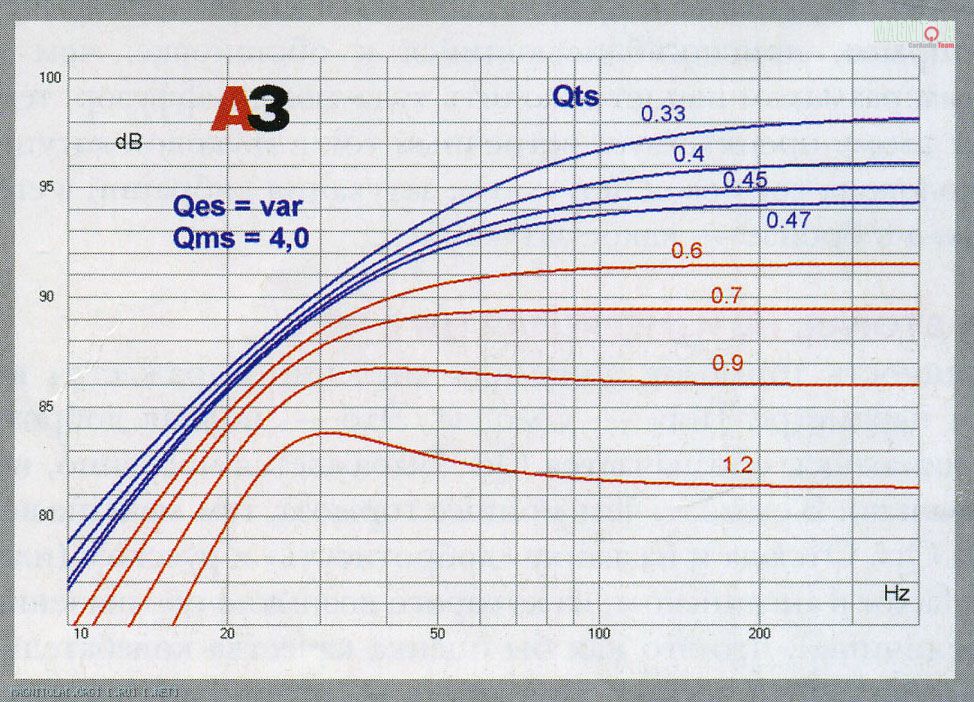
Те же значения Qts, но теперь всюду Qms = 4, а Qes меняется так, чтобы выйти на те же значения Qts. Значения Qts те же, а кривые совсем другие и различаются между собой намного меньше. Нижние, красные кривые получены для тех значений, которые нельзя было получить в первом опыте при фиксированной Qes = 0,5 | Кривые звукового давления для разных Qts, полученных изменением Qes. Четыре верхние кривые по форме — точно такие же, как когда мы меняли Qms, их форма определяется значениями Qts, а они остались прежними. Нижние, красные кривые, полученные для Qts больше 0,5, разумеется, другие, и на них начинает расти горб, обусловленный повышенной добротностью. |
А вот теперь обратите внимание: дело не только в том, что при высоких Qts на характеристике появляется горб, при этом снижается чувствительность динамика на частотах выше резонансной. Объяснение простое: при прочих равных Qes может возрастать только с ростом массы подвижной системы или с уменьшением мощности магнита. И то и другое ведёт к падению чувствительности на средних частотах. Так что горб на резонансной частоте — это, скорее, следствие провала на частотах выше резонансной. В акустике ничего бесплатного не бывает...
ВЕШАТЬ ИЛИ НЕ ВЕШАТЬ?
Образное определение условий измерения Fs как резонансной частоты динамика, висящего в воздухе, породило заблуждение, что так и надо эту частоту измерять, и энтузиасты норовили действительно подвешивать динамики на проволоках и верёвках. Измерениям параметров акустики будет посвящён отдельный выпуск «ВВ», а то и не один, здесь же отмечу: в грамотных лабораториях динамики при измерениях зажимают в тиски, а не подвешивают к люстре.
ВКЛАД МЛАДШЕГО ПАРТНЁРА
Между прочим: основоположник метода А.Н. Тиль намеревался учитывать в расчётах только электрическую добротность, полагая (справедливо для своего времени), что доля механических потерь пренебрежимо мала по сравнению с потерями, вызванными работой «электрического тормоза» динамика. Вклад младшего партнёра, не единственный, впрочем, заключался в учёте Qms, теперь это стало важным: в современных головках используются материалы с повышенными потерями, которых не было в начале 60-х, и нам попадались динамики, где величина Qms составляла всего лишь 2 — 3, при электрической под единицу. При таких делах не учитывать механические потери было бы ошибкой. И особенно важным это стало с внедрением феррожидкостного охлаждения в ВЧ-головках, там из-за демпфирующего действия жидкости доля Qms в полной добротности становится решающей, а пик импеданса на частоте резонанса становится почти не виден, как на первом графике нашего вычислительного эксперимента.
ТРИ КАРТЫ, ОТКРЫТЫЕ ТИЛЕМ И СМОЛЛОМ
1. Fs — частота основного резонанса динамика без всякого корпуса. Характеризует только сам динамик, а не готовую акустическую систему на его базе. При установке в любой объём может только возрастать.
2. Qts — полная добротность динамика, безразмерная величина, характеризующая относительные потери в динамике. Чем она ниже, тем больше подавлен резонанс излучения и тем выше пик сопротивления на импедансной кривой. При установке в закрытый ящик возрастает.
3. Vas — эквивалентный объём динамика. Равен объёму воздуха с такой же жёсткостью, что и у подвеса. Чем жёстче подвес, тем меньше Vas. При одной и той же жёсткости Vas растёт с ростом площади диффузора.
ДВЕ ПОЛОВИНКИ, СОСТАВЛЯЮЩИЕ КАРТУ №2
1. Qes — электрическая составляющая полной добротности, характеризует мощность электрического тормоза, препятствующего раскачке диффузора вблизи резонансной частоты. Обычно чем мощнее магнитная система, тем сильнее «тормоз» и тем меньше численно величина Qes.
2. Qms — механическая составляющая полной добротности, характеризует потери в упругих элементах подвеса. Потерь здесь намного меньше, чем в электрической составляющей, и численно Qms гораздо больше Qes.
КАРТА ТРЕТЬЯ, ОБЪЁМНАЯ
Как измеряют Vas — история отдельная, там есть забавные повороты, и об этом, как говорю уже в третий раз, будет в специальном выпуске серии. Для практики важно понять две вещи. Первая: предельно лоховское заблуждение (увы, тем не менее встречающееся), что приведенное в сопроводительных документах к динамику значение Vas — это объём, в который динамик надо ставить. А это всего лишь — характеристика динамика, зависящая только от двух величин: жёсткости подвеса и диаметра диффузора. Если поставить динамик в ящик с объёмом, равным Vas, резонансная частота и полная добротность возрастут в 1,4 раза (это квадратный корень из двух). Если в объём, равный половине Vas — в 1,7 раза (корень из трёх). Если сделать ящик объёмом в одну треть от Vas, всё остальное возрастёт вдвое (корень из четырёх, логика должна быть уже понятна и без формул).
В результате, действительно, чем меньше при прочих равных величина Vas у динамика, тем на более компактное оформление можно рассчитывать, сохраняя плановые показатели по Fc и Qtc. Компактность, однако, не даётся бесплатно. В акустике бесплатного вообще не бывает. Малое значение Vas при той же резонансной частоте динамика — результат сочетания жёсткого подвеса с тяжёлой подвижной системой. А от массы «подвижки» самым решительным образом зависит чувствительность. Поэтому все сабвуферные головки, отличающиеся возможностью работы в компактных закрытых корпусах, характеризуются и низкой чувствительностью по сравнению с коллегами с лёгкими диффузорами, но большими значениями Vas. Так что хороших и плохих значений Vas тоже не бывает, всему своя цена.
О чём пойдёт разговор в следующий раз? Понятно, о чём. Карты знаем, теперь — как сдавать, с какой ходить...
Источник: журнал Автозвук, 03/2005. Андрей Елютин


 Рубрики
Рубрики Новое в каталоге
Новое в каталоге




 Категории
Категории